Math Art

This lesson will create an AI artist, and show how fun math can be, by creating creative circle (trig) artist! Do not worry, you can use this lesson even if you do not understand trigonometry.

Prerequisite

You must have basic understanding of coding and have completed the Drawing lesson and know about Functions.

A Circle

There are many ways to draw circles very effectively, but this lesson will rely on the basics and use Sin and Cos. All you need to know is that these return a point around a circle. You give them an angle around a circle and they return a point. They assume the circle has a size (diameter) of 1, but we can multiply the results with the desired diameter.

In C# Sin() and Cos() functions are available in the Math class found under the System namespace. We need to add using System; to the top of our code. Finally, Sin() and Cos() take angles in radians. We will add a function that converts degrees to radians.

In Python math.cos() and math.sin() are available by adding import math to the top of our program.

In JavaScript, The DtoR function converts degrees to radians, a necessary step for trigonometric calculations.

A circle is 360 degrees and so our loop will go from 0 to 360 and draw the points.

Python

import math

def DtoR(degree):
    radians = (math.pi / 180) * degree
    return radians

BrainPad.Display.Clear(0)
a = 0.0
while a < 360:
    circleX = math.cos(DtoR(a)) * 30
    circleY = math.sin(DtoR(a)) * 30
    BrainPad.Display.SetPixel(1, circleX, circleY)
    a = a + 1
    BrainPad.Display.Show()

C#

double DtoR(double degree) {
    var radians = (Math.PI / 180) * degree;
    return radians;
}

BrainPad.Display.Clear(0);
var a = 0.0;
while (a < 360) {
    var circleX = Math.Cos(DtoR(a)) * 30;
    var circleY = Math.Sin(DtoR(a)) * 30;
    BrainPad.Display.SetPixel(1, (int)circleX, (int)circleY);
    a = a + 1;
    BrainPad.Display.Show();
}

JS

function DtoR(degree) {
    let radians = (Math.PI / 180) * degree;
    return radians;
}

await BrainPad.Display.Clear(0);
let a = 0.0;
while (a < 360) {
    let circleX = Math.cos(DtoR(a)) * 30;
    let circleY = Math.sin(DtoR(a)) * 30;
    await BrainPad.Display.SetPixel(1, circleX, circleY);
    a = a + 1;
    await BrainPad.Display.Show();
}

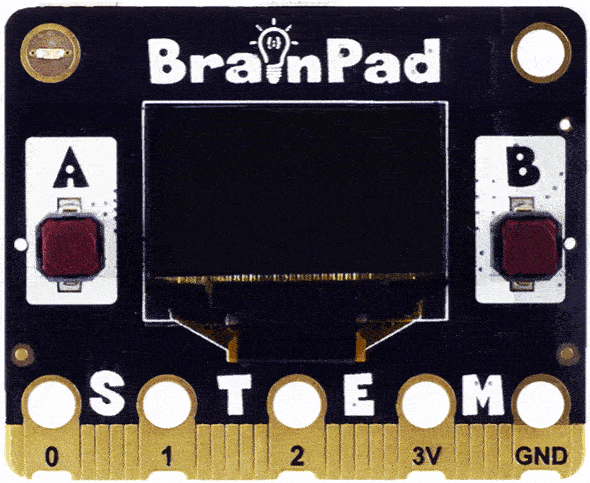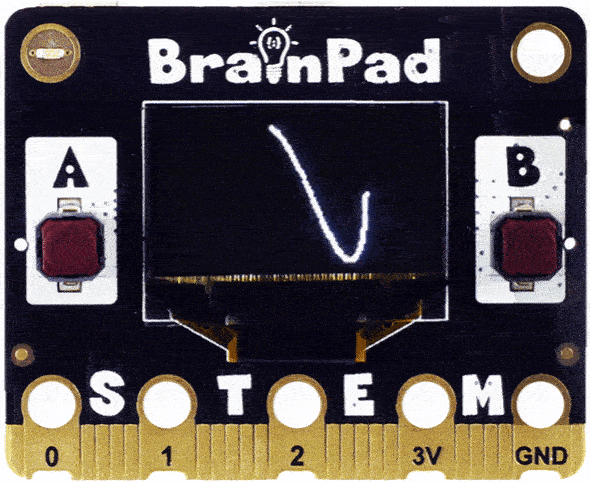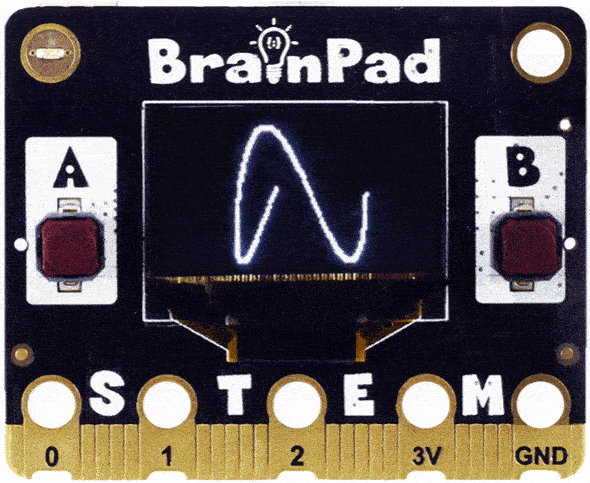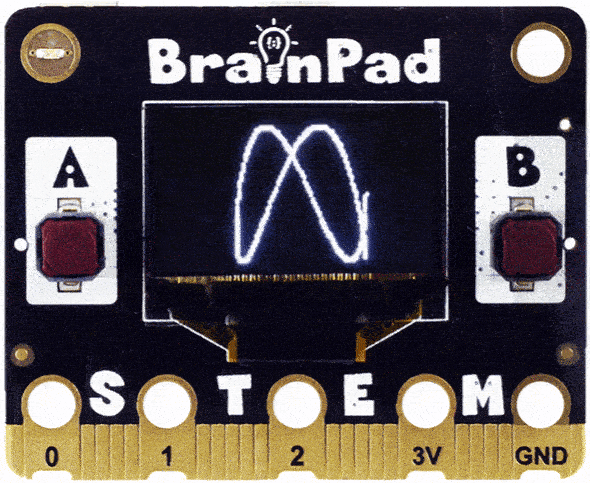
Oh look, we have a circle… sort of! The circle is positioned at 0,0 so we are only seeing a quarter of it. We can shift the circle to the middle of the screen.

Note that we will omit the using & import statement going forward. We will also omit the DtoR() function.

Python

BrainPad.Display.Clear(0)
a = 0.0
while a < 360:
    circleX = math.cos(DtoR(a)) * 30
    circleY = math.sin(DtoR(a)) * 30
    BrainPad.Display.SetPixel(1, 64+circleX, 32+circleY)
    a = a + 1
    BrainPad.Display.Show()

C#

BrainPad.Display.Clear(0);
var a = 0.0;
while (a < 360) {
    var circleX = Math.Cos(DtoR(a)) * 30;
    var circleY = Math.Sin(DtoR(a)) * 30;
    BrainPad.Display.SetPixel(1, (int)circleX+64, (int)circleY+32);
    a = a + 1;
    BrainPad.Display.Show();
}

JS

await BrainPad.Display.Clear(0);
let a = 0.0;
while (a < 360) {
    let circleX = Math.cos(DtoR(a)) * 30;
    let circleY = Math.sin(DtoR(a)) * 30;
    await BrainPad.Display.SetPixel(1, circleX+64, circleY+32);
    a = a + 1;
    await BrainPad.Display.Show();
}

Trig Race

What happens if Sin() is going twice as fast as Cos()? We do this by multiplying the angle by 2. This is making one angle go twice as fast as the other.

Python

BrainPad.Display.Clear(0)
a=0.0

while a < 360:
    circleX = math.cos(DtoR(a)) * 30
    circleY = math.sin(DtoR(a*2)) * 30
    BrainPad.Display.SetPixel(1, circleX+64, circleY+32)
    a = a + 1
    BrainPad.Display.Show()

C#

BrainPad.Display.Clear(0);
var a=0.0;

while (a < 360) {
    var circleX = Math.Cos(DtoR(a)) * 30;
    var circleY = Math.Sin(DtoR(a*2)) * 30;
    BrainPad.Display.SetPixel(1, (int)circleX+64, (int)circleY+32);
    a = a + 1;
    BrainPad.Display.Show();
}

JS

await BrainPad.Display.Clear(0);
let a = 0.0;
while (a < 360) {
    let circleX = Math.cos(DtoR(a)) * 30;
    let circleY = Math.sin(DtoR(a*2)) * 30;
    await BrainPad.Display.SetPixel(1, circleX+64, circleY+32);
    a = a + 1;
    await BrainPad.Display.Show();
}

Do you see how the circle got folded in and now we have an infinity symbol? Change the code to 3 times faster. Do you see three curves?

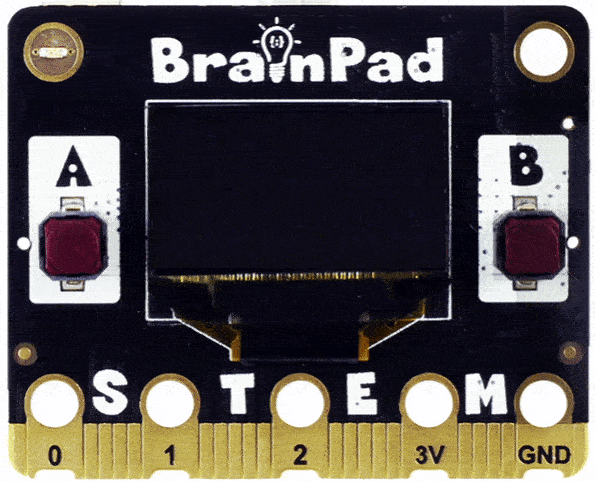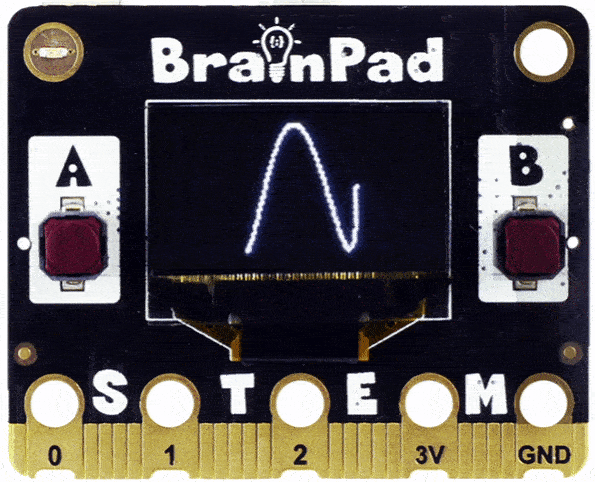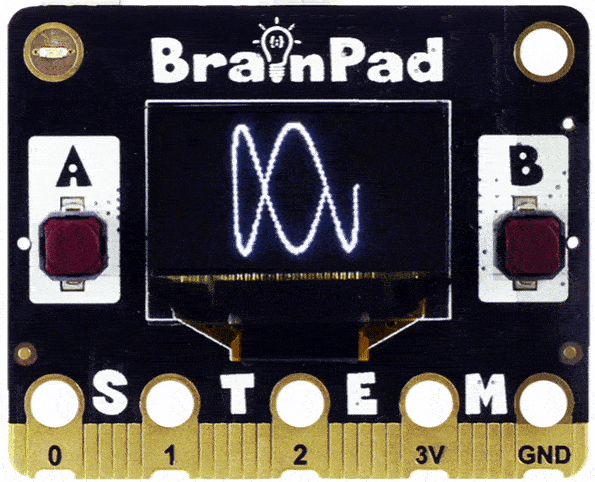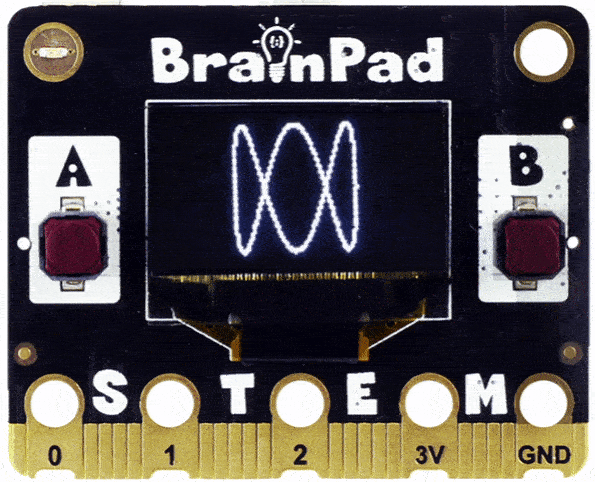
Can you guess what 4 or 5 would look like?

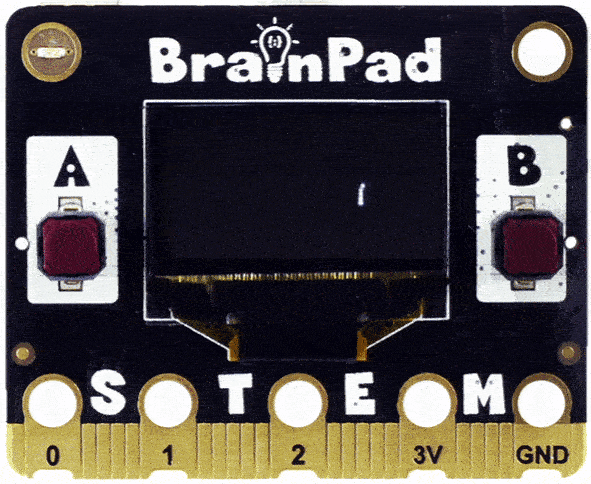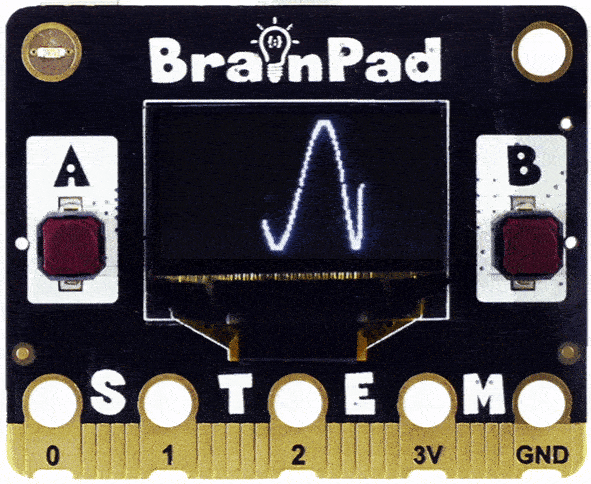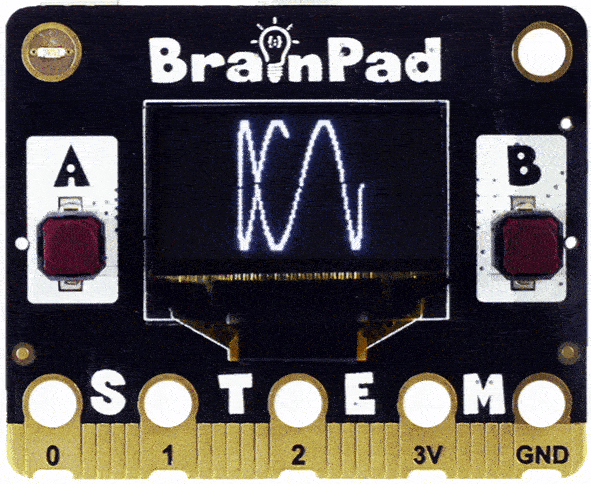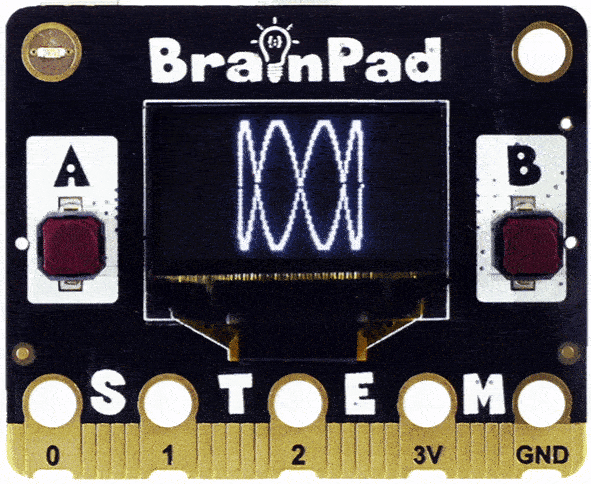
You may have guessed right, but what if you use 2.2?

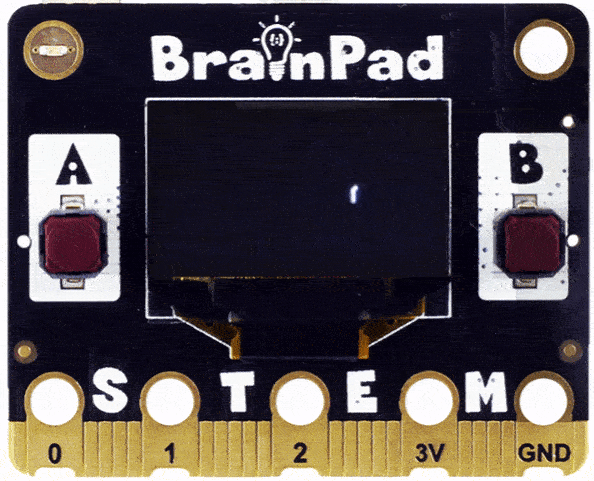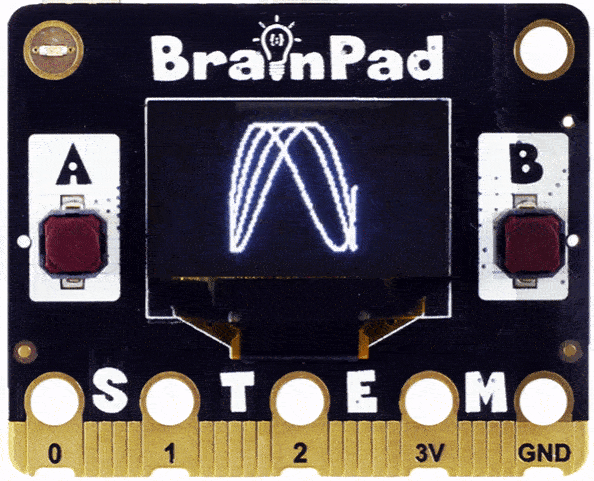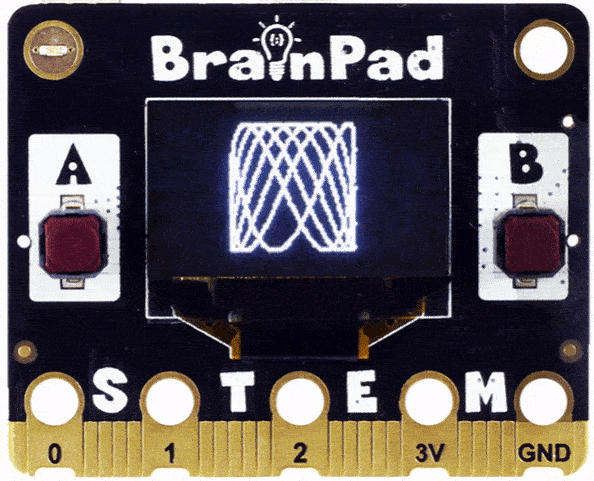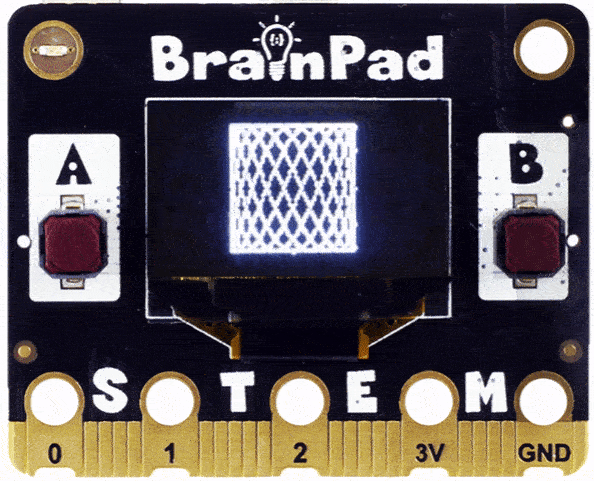
Looks like we are onto something, but the drawing was not complete. This is because the 2.0 will complete, but then the fraction 0.2 will not get a whole round. For 0.2 to become 1 (full round) you need to repeat our loop 5 times.

Python

BrainPad.Display.Clear(0)
a=0.0

while a < 360 * 5:
    circleX = math.cos(DtoR(a)) * 30
    circleY = math.sin(DtoR(a*2.2)) * 30
    BrainPad.Display.SetPixel(1, circleX+64, circleY+32)
    a = a + 1
    BrainPad.Display.Show()

C#

BrainPad.Display.Clear(0);
var a=0.0;
while (a < 360 * 5) {
    var circleX = Math.Cos(DtoR(a)) * 30;
    var circleY = Math.Sin(DtoR(a*2.2)) * 30;
    BrainPad.Display.SetPixel(1, (int)circleX+64, (int)circleY+32);
    a = a + 1;
    BrainPad.Display.Show();
}

JS

await BrainPad.Display.Clear(0);
let a = 0.0;
while (a < 360*5) {
    let circleX = Math.cos(DtoR(a)) * 30;
    let circleY = Math.sin(DtoR(a*2.2)) * 30;
    await BrainPad.Display.SetPixel(1, circleX+64, circleY+32);
    a = a + 1;
    await BrainPad.Display.Show();
}

Circle of Circles

A circle can become all kinds of interesting shapes on its own, but what if we made a circle spiral along the circumference of another circle? The spiraling circle should go faster than the other circle it is going around. If not faster, then we will just have a larger circle. We will try 2 times faster and see what the results may look like.

Python

BrainPad.Display.Clear(0)
a=0.0

while a < 360:
    circleX = math.cos(DtoR(a)) * 20
    circleY = math.sin(DtoR(a)) * 20
    spiralX = math.cos(DtoR(a * 2)) * 10
    spiralY = math.sin(DtoR(a * 2)) * 10
    BrainPad.Display.SetPixel(1, circleX+spiralX+64, circleY+spiralY+32)
    a = a + 1
    BrainPad.Display.Show()

C#

BrainPad.Display.Clear(0);
var a=0.0;

while (a < 360) {
    var circleX = Math.Cos(DtoR(a)) * 20;
    var circleY = Math.Sin(DtoR(a)) * 20;
    var spiralX = Math.Cos(DtoR(a * 2)) * 10;
    var spiralY = Math.Sin(DtoR(a * 2)) * 10;
    BrainPad.Display.SetPixel(1, (int)(circleX+spiralX + 64), (int)(circleY+ spiralY + 32));
    a = a + 1;
    BrainPad.Display.Show();
}

JS

await BrainPad.Display.Clear(0);
let a = 0.0;
while (a < 360) {
    let circleX = Math.cos(DtoR(a)) * 20;
    let circleY = Math.sin(DtoR(a)) * 20;
    let spiralX = Math.cos(DtoR(a * 2)) * 10;
    let spiralY = Math.sin(DtoR(a * 2)) * 10;
    await BrainPad.Display.SetPixel(1, circleX+spiralX+64, circleY+spiralY+32);
    a = a + 1;
    await BrainPad.Display.Show();
}

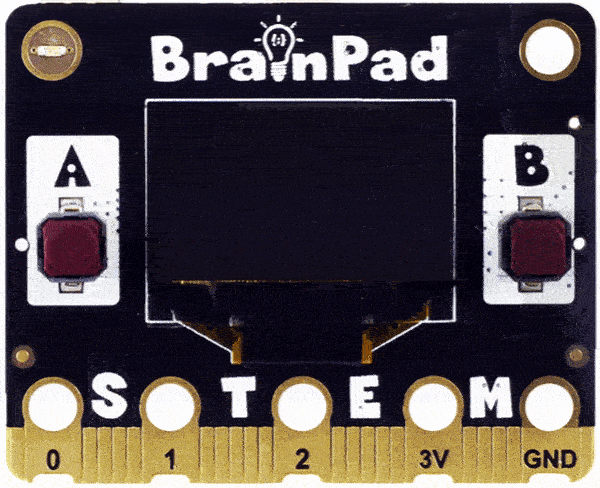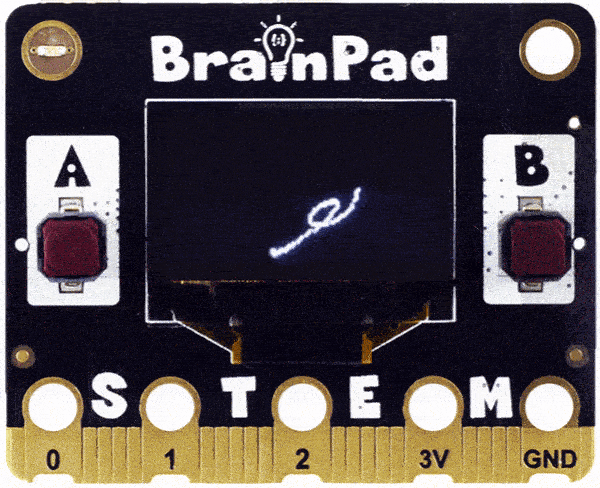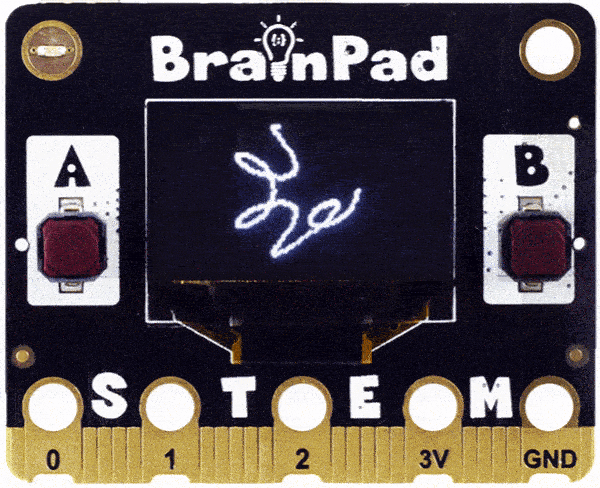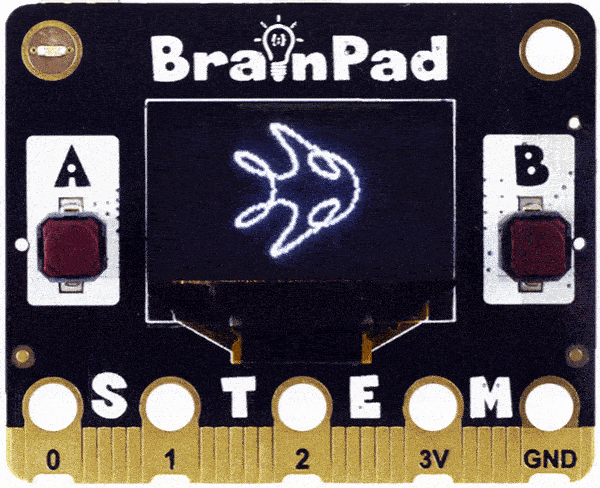
Is that a badly shaped heart? Change the multiplier of the spiral to 3, 4, 5… etc. Can you visualize what is happening? Here is what 15 would look like.

You can see what the circle is doing, but here is something impossible to visualize! What if we did 6 multiplier for spiralX but then used 5 for spiralY?

Python

BrainPad.Display.Clear(0)
a=0.0

while a < 360 * 5:
    circleX = math.cos(DtoR(a)) * 20
    circleY = math.sin(DtoR(a)) * 20
    spiralX = math.cos(DtoR(a * 6)) * 10
    spiralY = math.sin(DtoR(a * 5)) * 10
    BrainPad.Display.SetPixel(1, circleX+spiralX+64, circleY+spiralY+32)
    a = a + 1
    BrainPad.Display.Show()

C#

BrainPad.Display.Clear(0);
var a=0.0;

while (a < 360 * 5) {
    var circleX = Math.Cos(DtoR(a)) * 20;
    var circleY = Math.Sin(DtoR(a)) * 20;
    var spiralX = Math.Cos(DtoR(a * 6)) * 10;
    var spiralY = Math.Sin(DtoR(a * 5)) * 10;
    BrainPad.Display.SetPixel(1, (int)(circleX+spiralX + 64), (int)(circleY+ spiralY + 32));
    a = a + 1;
    BrainPad.Display.Show();
}

JS

await BrainPad.Display.Clear(0);
let a = 0.0;
while (a < 360) {
    let circleX = Math.cos(DtoR(a)) * 20;
    let circleY = Math.sin(DtoR(a)) * 20;
    let spiralX = Math.cos(DtoR(a * 5)) * 10;
    let spiralY = Math.sin(DtoR(a * 6)) * 10;
    await BrainPad.Display.SetPixel(1, circleX+spiralX+64, circleY+spiralY+32);
    a = a + 1;
    await BrainPad.Display.Show();
}

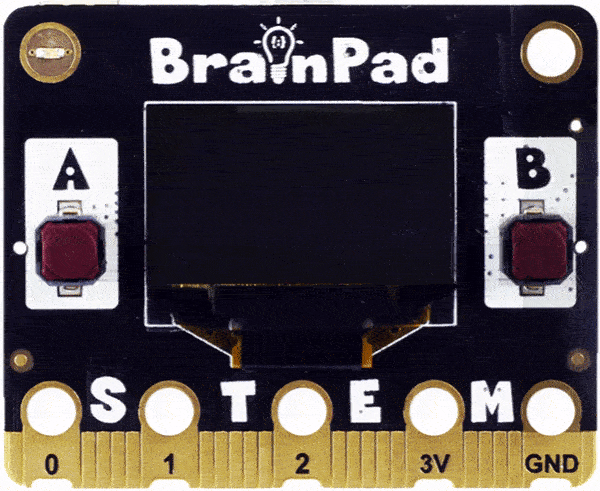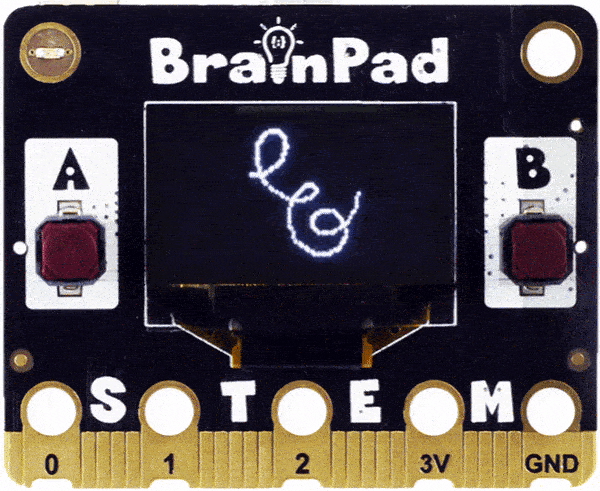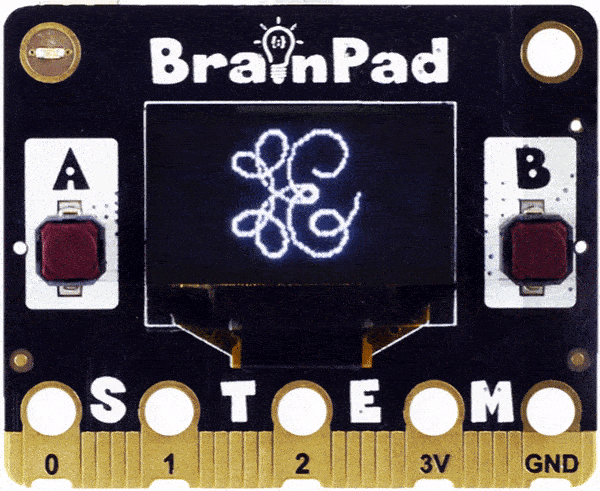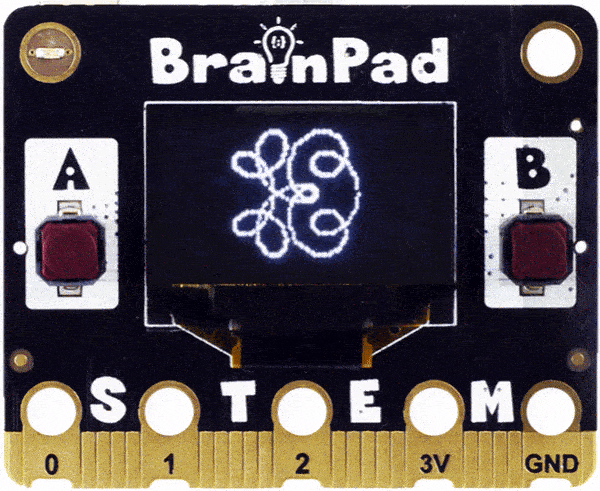
We bet you have never seen math this cool before! Ok, let’s do it the other way around. Keep the same multiplier for the spiral and change it for the circle being surrounded.

Python

BrainPad.Display.Clear(0)
a=0.0

while a < 360 * 5:
    circleX = math.cos(DtoR(a)) * 20
    circleY = math.sin(DtoR(a * 2)) * 20
    spiralX = math.cos(DtoR(a * 8)) * 10
    spiralY = math.sin(DtoR(a * 8)) * 10
    BrainPad.Display.SetPixel(1, circleX+spiralX+64, circleY+spiralY+32)
    a = a + 1
    BrainPad.Display.Show()

C#

BrainPad.Display.Clear(0);
var a=0.0;

while (a < 360 * 5) {
    var circleX = Math.Cos(DtoR(a)) * 20;
    var circleY = Math.Sin(DtoR(a*2)) * 20;
    var spiralX = Math.Cos(DtoR(a * 8)) * 10;
    var spiralY = Math.Sin(DtoR(a * 8)) * 10;
    BrainPad.Display.SetPixel(1, (int)(circleX+spiralX + 64), (int)(circleY+ spiralY + 32));
    a = a + 1;
    BrainPad.Display.Show();
}

JS

await BrainPad.Display.Clear(0);
let a = 0.0;
while (a < 360) {
    let circleX = Math.cos(DtoR(a)) * 20;
    let circleY = Math.sin(DtoR(a * 2)) * 20;
    let spiralX = Math.cos(DtoR(a * 8)) * 10;
    let spiralY = Math.sin(DtoR(a * 8)) * 10;
    await BrainPad.Display.SetPixel(1, circleX+spiralX+64, circleY+spiralY+32);
    a = a + 1;
    await BrainPad.Display.Show();
}

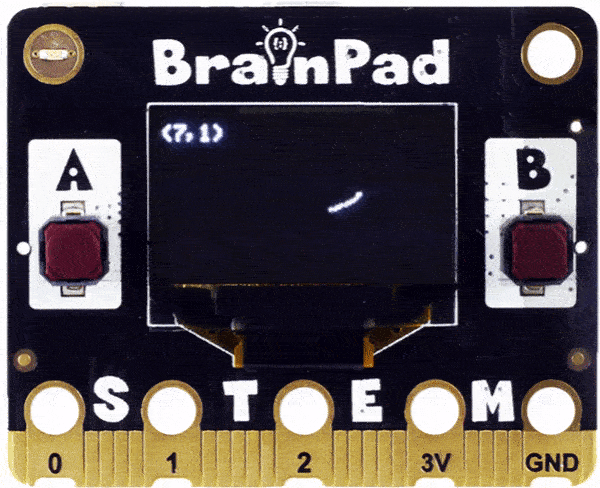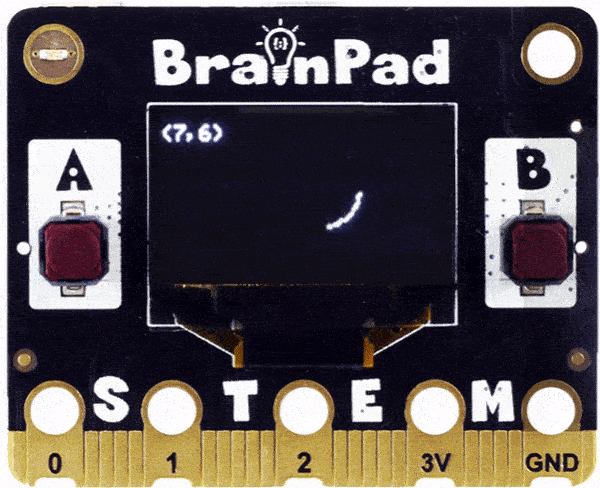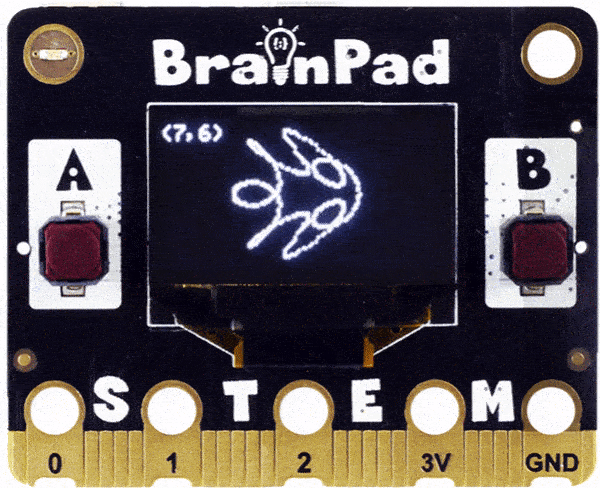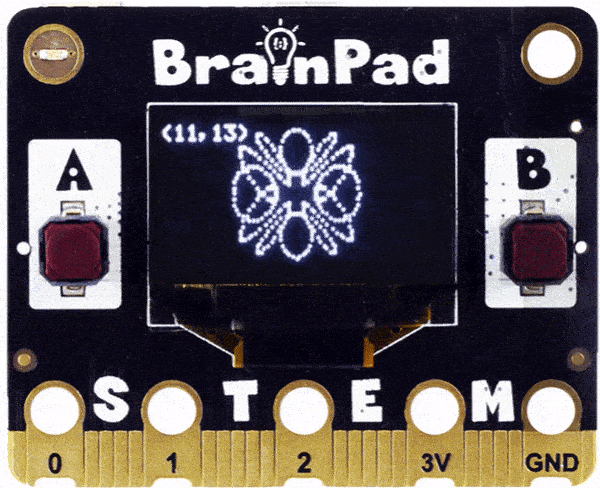
There are hours of fun still! Can you change one of the numbers to be a random number and let the code clear the screen and draw a new shape nonstop?

Python

import random

def DtoR(degree):
    radians = (math.pi / 180) * degree
    return radians


while True:
    BrainPad.Display.Clear(0)
    a = 0.0
    randX = random.randint(1,15)
    randY = random.randint(1,15)
    BrainPad.Display.DrawText("(" + str(randX) + "," + str(randY) + ")", 1, 0, 0)
 
    while a < 360:
        circleX = math.cos(DtoR(a)) * 20
        circleY = math.sin(DtoR(a)) * 20
        spiralX = math.cos(DtoR(a * randX)) * 10
        spiralY = math.sin(DtoR(a * randY)) * 10

        BrainPad.Display.SetPixel(1, circleX+spiralX+64, circleY+spiralY+32)
        a = a + 1
        BrainPad.Display.Show()
    BrainPad.System.Wait(2000)

C#

double DtoR(double degree) {
    var radians = (Math.PI / 180) * degree;
    return radians;
}

var rnd = new Random();
while(true)
{
    BrainPad.Display.Clear(0);
    var a=0.0;
    var randX = rnd.Next(15) + 1;
    var randY = rnd.Next(15) + 1;
    BrainPad.Display.DrawText("(" + randX + "," + randY + ")", 1, 0, 0);
    while (a < 360) {
        var circleX = Math.Cos(DtoR(a)) * 20;
        var circleY = Math.Sin(DtoR(a)) * 20;
        var spiralX = Math.Cos(DtoR(a * randX)) * 10;
        var spiralY = Math.Sin(DtoR(a * randY)) * 10;
        BrainPad.Display.SetPixel(1, (int)(circleX+spiralX + 64), (int)(circleY+ spiralY + 32));
        a = a + 1;
        BrainPad.Display.Show();
    }
    BrainPad.System.Wait(2000);
}

JS


function DtoR(degree) {
    var radians = (Math.PI / 180) * degree;
    return radians;
}

while(true)
{
    await BrainPad.Display.Clear(0);
    let a = 0.0;
    var randX = Math.floor(Math.random()*15) + 1;
    var randY = Math.floor(Math.random()*15) + 1;
    await BrainPad.Display.DrawText("(" + randX + "," + randY + ")", 1, 0, 0);
    while (a < 360) {
        let circleX = Math.cos(DtoR(a)) * 20;
        let circleY = Math.sin(DtoR(a)) * 20;
        let spiralX = Math.cos(DtoR(a * randX)) * 10;
        let spiralY = Math.sin(DtoR(a * randY)) * 10;
        await BrainPad.Display.SetPixel(1, circleX+spiralX+64, circleY+spiralY+32);
        a = a + 1;
        await BrainPad.Display.Show();
    }
    await BrainPad.System.Wait(2000);
}

What’s Next?

Are you ready for some game-making? Jump back to Python, C#, and JS Coding Lessons.

BrainStorm

Who knew math could be so creative on its own?! Some of these drawings start as completely random but are completed beautifully.